Root Cause Analysis
Introduction
Anomaly detection (AD) and root cause analysis (RCA) in multivariate time series refer to the recognition of abnormalities in data and the identification of their root causes. RCA, without the underpinning of anomaly detection, loses its meaning. Similarly, anomaly detection, without the explanation provided by RCA, loses much of its explainability and actionability. Detected anomalies can be interpreted as suggestions of where to investigate in the data—suspicious data points to check—and the corresponding root causes can then be seen as the directions in which to inquire—potential explanations to analyze. The combination of AD and RCA can assist analysts in making critical decisions and prioritizing their limited attention on the most valuable and impactful insights their data can offer at each moment.
For meaningful RCA, the system should capture relationships between time series, be robust to overfitting and noise, provide a transparent and explainable model, and return varying levels of anomaly scores based on the severity of different incidents to dispatchers. TIM addresses these challenges collectively.
Output
In the example provided below, there is a table representing the output of the root cause analysis:
| timestamp | term_1 | term_2 | term_3 | … | term_N | yhat_1 | yhat_2 | yhat_3 | … | yhat_N | predictor_1 | predictor_2 | predictor_3 | … | predictor_N |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2014-10-25T04:00:00.0 | 2546 | 900 | 943.05 | … | 624 | 1943 | 1984 | 1987 | … | 3296 | 1443 | 1984 | 1287 | … | 1396 |
| 2014-10-26T04:00:00.0 | 2451 | 5000 | 5409.6 | … | 234 | 2195 | 2104 | 2089 | … | 3123 | 2943 | 1584 | 2987 | … | 1496 |
| 2014-10-27T04:00:00.0 | 2103 | 200 | 65363.4 | … | 123 | 2211 | 2190 | 2168 | … | 2762 | 2142 | 1984 | 2987 | … | 996 |
| 2014-10-28T04:00:00.0 | 2301 | 100 | 543.5 | … | 545 | 2189 | 2154 | 2167 | … | 4153 | 643 | 1984 | 1987 | … | 1996 |
| 2014-10-29T04:00:00.0 | 2225 | 432 | 983 | … | 321 | 2567 | 2592 | 2598 | … | 3112 | 1143 | 1484 | 1987 | … | 1996 |
| 2014-10-30T04:00:00.0 | 2155 | 4355 | 1235.6 | … | 134 | 2532 | 2490 | 2487 | … | 4123 | 4943 | 1984 | 1987 | … | 1996 |
Benefits
RCA provides additional information regarding anomalies.
Without RCA, a user can examine the actual values compared to the normal behavior values, the detected anomalies, the influencers, and the anomaly indicator(s). However, there would be no information about potential reasons for any identified anomaly, which is introduced when considering the RCA results.
An example is depicted in the image below:
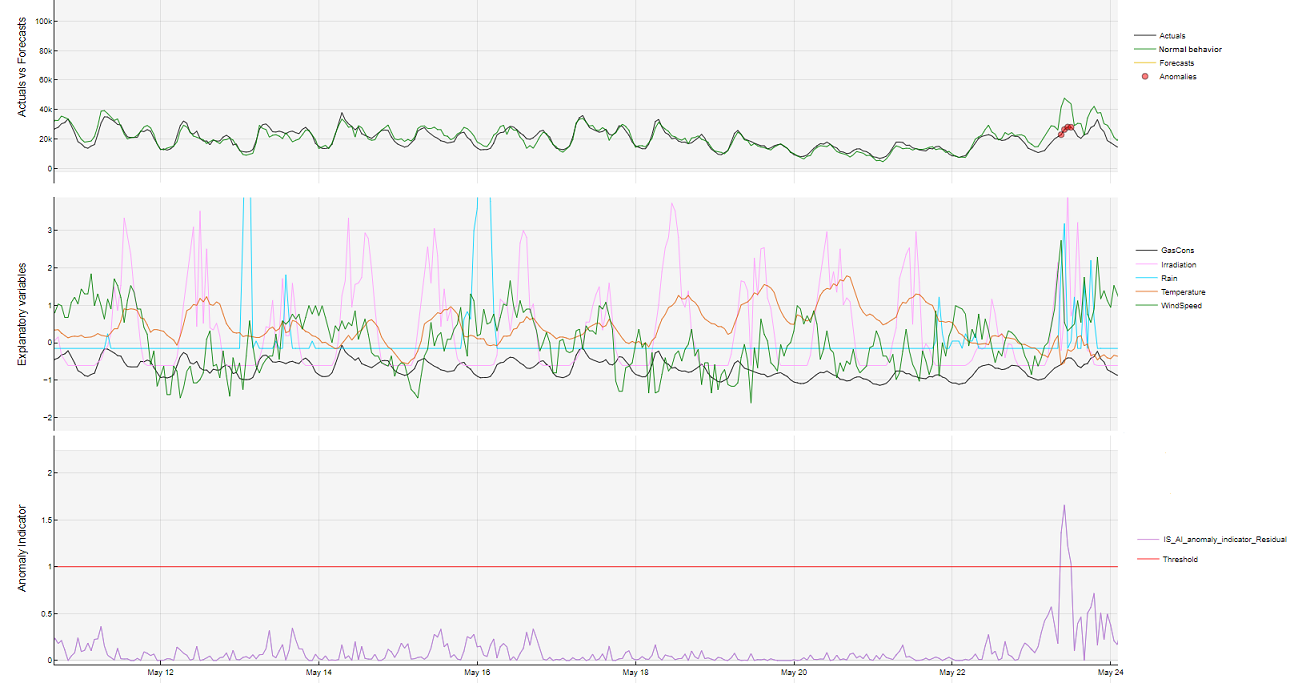
It is evident that something unusual occurred on May 23rd. The anomaly indicator surpassed the threshold, and the disparity between the actual values and the expected values is more pronounced compared to the surrounding observations. The top line chart is marked with red dots indicating an anomaly. However, the cause behind this increase in normal behavior remains unclear.
The primary objective of RCA is to provide information that investigates the factors influencing the increase in normal behavior. When an uncommon difference between the actual value and the expected value leads to the detection of an anomaly, RCA helps a user assess the relevance of the influencer's and term's contributions. Suspicious factors can be identified, prompting an examination of the accuracy of the data measurements. This analysis can lead to the conclusion that there is an issue with the influencer(s) or the model term(s), or that they are correct and the problem lies with the value of the KPI. In the latter case, it implies that the KPI did not follow the expected normal behavior, but should. This knowledge can be valuable when making critical decisions, such as whether or not to initiate an inspection of the machine/component associated with the given KPI.
In summary, RCA offers a user:
- Transparency, explainability, and confidence in results for making critical decisions.
- Deeper insights into the factors driving normal behavior.
- The ability to explore potential causes behind detected anomalies.
- Trust to make the final decision regarding anomaly candidates based on further analysis.
Interpreting root cause analysis results
First and foremost, it is important to note that each normal behavior value can be generated by a different model within a Model Zoo. When examining the normal behavior and comprehending its construction, it is necessary to restrict the view to only other normal behavior values generated by the exact same model. This is why the model's index is a required parameter in the RCA endpoint. Each model's terms are additive, allowing for a clear understanding of the individual impact of each term on the normal behavior. There are three distinct views available: the nominal term view, the relative term view, and the influencer view.
The nominal term view provides precise information regarding the contribution of each term to the estimated normal behavior value. The relative term view presents a slightly different decomposition of the normal behavior, facilitating a better geometrical understanding of how the model gradually takes shape by adding terms. The influencer view aggregates the impact of each influencer across all terms in the model, offering information on the contribution of each influencer to the normal behavior value.
Nominal term_i
The value of the i-th term of the model of a chosen model_index used to obtain the normal behavior. The term can be found in the Model Zoo by model_index and the order number i. It is essential to mention that the term1 of the model with the _model_index 1 is different than the term1 of the model with the _model_index 2 - they are two separate models and have different terms.
NOTE: For a given timestamp t, the sum of the terms equals the normal behavior value.
Relative yhat_i
This essentially equals the normal behavior which would be obtained if the model only consisted of the first i terms (different from the sum of the first i terms). The forecasting error thus decreases with increasing i, showing the gradual build-up of the model. The nominal view of terms does not satisfy this property. This property visualizes how important individual terms are for the final normal behavior and how they influence it. If something goes wrong, this allows users to easily identify which term is responsible.
NOTE: For a given timestamp t, the last yhat (cumulation of all yhat's) equals the normal behavior value.
Aggregated influencer_i
It reveals the involvement of i-th influencer in the normal behavior value for a given data point. This is a straightforward way to figure out the impact of a given influencer on the normal behavior value.
NOTE: For a given timestamp t, the sum of the influencers equals the normal behavior value.